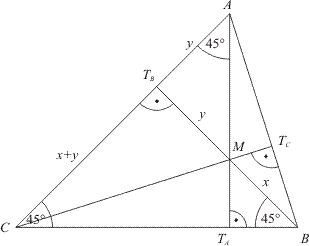
A geometriában a háromszög olyan sokszög, aminek három oldala, másként fogalmazva három csúcsa van. Ez volt a háromszög definíciója. Ez a bejegyzés azonban nem a matematikáról, jobban mondva a geometriáról fog szólni, hanem másról, amihez bizony köze van a háromszögeknek. És, hogy egy kis PTI is legyen benne ezért változókat fogok alkalmazni, de típus nélkül fogom deklarálni, úgyis ki fog derülni. Itt fontos leszögeznem, hogy nincsen benne típuskeveredés :).
Mivel köztudott, hogy a háromszög egyenesekből áll, egy egyenest pedig 2 pont határoz meg, ezért egy harmadik már nem férne rá, s ha közötte lenne, akkor nem áll össze a háromszög, ami egyáltalán nem baj, hiszen az egyenesek a 2 ponttal, valahogy szebbek és jobbak :).
Először legyen n,k,e háromszög. Most tegyük fel, hogy e akar egy közös egyenest alkotni n-el, de n-nek van egy pár nagyon halvány vonala k-hoz. Sajnos a radír nem tudta eltörölni így, jó ideig maradt a háromszög, azonban szétbomláskor az n,k egyenes jött létre. e egy magányos pontot alkot, valahol a szabadvektorok terén.
Másodszor legyen egy j,a,e háromszög. Ebben az esetben tegyük, fel, hogy e akar egy közös egyenest alkotni j-vel, azonban az egyenesek helyett egy pár pillanatig egy háromszög látszik kirajzolódni, majd létre is jön. Ekkor több ütközet után, a szétbomláskor végülis a j,a – egyenes fog együvé tartozni és e ismét marad egyedül, magányosan a szabadvektorok terén.
Következő háromszög, talán a legtöbb ideig tartott, de ez már olyan háromszög, ami szinte négyzet, ami ráadásul tartalmaz egy belső kört is. A háromszög betűjelzése legyen t,f,e. A négyzeté legyen t,w,f,e. A körbe tartozzon h és s. Klasszikus felállás, t, f-en keresztül megismeri e-t aztán közben f-el egy kis ideig egy egyenest alkotnak, majd marad a két ont a síkon legyen ez a sík egy lineáris altér. e szétnéz az előbb említett altéren, ahol meglátja t-t, s utána össze is ismerkednek, ekkor valahogyan visszavándorol szabadvektorok alteréről f, s már szerkeszthető is lenne a háromszög. DE, miután nagyjából létrejött a triangulum, bekerült egy külső ponthalmazból f által w. A belső kör csak közvetítő szerepet töltött be, ezt nagyon fontos tudni. Miután létrejött a négyzet, majdnem ideálisan bomlott fel. 2-2 szép egyenesre. De nem így lett. Szétbomlott egy egyenesre, s két pontra, de tudomásom szerint a 4. pont nem maradt a szabad vektorok terén. Így ez lett a felállás: t-f, egyenes, w pont, e pont. Természetesen az e pont került vissza a szabad vektorok terébe, ahol csak a kiindulópont volt adott, s az irány ismeretlen maradt. Mindmáig a végtelen felé konvergál ez az ismeretlen irányú e vektor.
Ezeket a háromszög sorokat sajnos a végtelenig folytathatnám, de az már-már áttekinthetetlenné és felfoghatatlanná tenné az egész irományt, melynek a végére egy kérdés maradt. Milyen típusúak a változtathatatlan változók?










Utolsó kommentek